Characterizing COVID-19 waves in urban and rural districts of India

Knowledge

COVID-19 knowledge

We use day by day district-level COVID-19 reported incidence knowledge (till July 31, 2021, based mostly on the waning of the second wave) from the COVID19India.org platform, a citizen-science-based knowledge assortment and validation effort, which has compiled incidences, recoveries, deaths, and vaccination knowledge from varied authorities and media stories. We preprocess the info to make sure nationwide protection and spatial consistency with Census knowledge. District-level knowledge is unavailable for a couple of States and Union Territories (Assam, Sikkim, Manipur, Telangana, Delhi, Goa, and Andaman & Nicobar Islands). Consequently, we disaggregate the info for these areas utilizing a population-weighted allocation of day by day incidence, knowledgeable by our statement of great correlations between (log) cumulative incidence and (log) inhabitants measurement (Pearson’s correlation coefficient = 0.73) and up to date scaling analyses utilized to COVID-19 incidences^38,39,40.

Demographic and concrete boundaries knowledge

We use the inhabitants dataset for 2020 from WorldPop with age groupings, owing to the absence of a latest Census dataset and given increased spatial decision (~100 m)⁴¹ in comparison with different candidate datasets similar to, Landscan⁴² and GPW⁴³. We combination this dataset (utilizing zonal statistics) to estimate complete inhabitants, inhabitants density, and common inhabitants age, on the district stage. As well as, we use 2018 International Human Settlement Layer Dataset (https://ghsl.jrc.ec.europa.eu/, at 10 m) to determine city areas (likelihood threshold = 0.1) and derive city inhabitants shares (% city) by combining with the WorldPop dataset.

Census knowledge

We use the 2011 Census (https://censusindia.gov.in) as the info supply for modes of journey to work (as a share of the working inhabitants commuting by a particular mode of transportation) and commuting patterns throughout districts in India. We concentrate on two variables for commuting patterns: the share of the working inhabitants with no commute. We calculate % employees working from residence for every district as a share share of the variety of employees with “No Journey” to the full working inhabitants. For the common commuting distance to work, we take the mid-point of the gap bins with most distance of 60 km). Owing to the absence of a latest dataset, we assume that the cross-sectional distributions of those traits stay invariant between 2011 and the temporal protection of the COVID-19 time collection.

Social media knowledge

We use Fb’s inhabitants motion knowledge⁴⁴ out there on the district stage and an 8-h frequency to estimate the scale of the incoming inhabitants through the period of the wave, based mostly on in-degree metric (in_degree_j) for every edge, i.e., district (j), of the community with V vertices (Eq. (1)).

Wealth knowledge

District-level earnings or wealth knowledge in India has restricted availability. The prevailing nationwide shopper expenditure surveys (CES) measure consumption-expenditure as an earnings proxy, which is much less dependable on the district stage as a result of restricted pattern measurement. This examine makes use of a family assets-based measure of wealth or dwelling requirements from the 2015–16 demographic and well being survey (DHS) with an approximated six instances higher pattern measurement than CES, with 601,509 sampled households. Accessible as a composite index on the family stage (https://dhsprogram.com/), we estimate weighted district-level common wealth index, utilizing sampling weights.

COVID-19 metrics throughout waves

COVID wave characterization

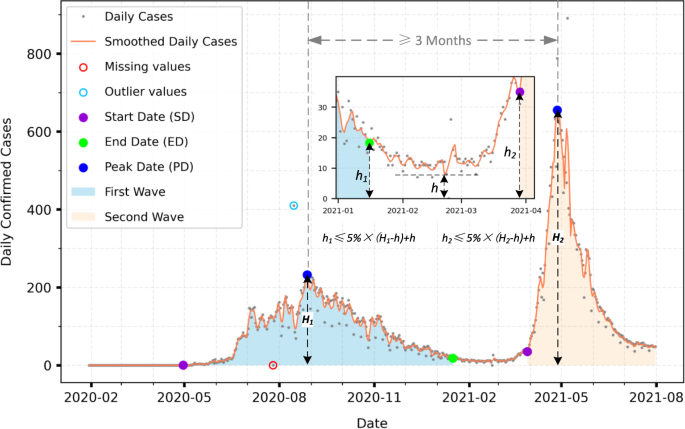
Earlier than characterizing the waves, we use two knowledge processing steps: preprocessing and wave metrics estimation. Preprocessing detects outliers, interpolates lacking values, and filters the time collection. Outlier detection identifies anomalous values inside a 14-day window based mostly on a ten% (P₁) and 90% (P₂) percentile vary (PR): PR = P₂ – P₁. We outline outliers as values falling beneath P₁ – 3PR or above P₂ + 3PR and linearly interpolate the outliers and different lacking values throughout the 14-day window (Fig. 4). To additional scale back noise, we use a Savitzky–Golay (SG) filter, which filters the time collection whereas preserving the form and top of the curve based mostly on least-squares polynomial approximation. SG filter has two essential parameters: window measurement and order of the polynomial. After trial and testing, we notice that utilizing small temporal window sizes and huge polynomial order retains noise within the time collection. Consequently, we choose 14 days because the optimum window measurement and a second-order polynomial within the SG filter. Throughout the wave metrics estimation, we concentrate on three metrics: peak date (PD_i), begin date (SD_i), and finish date (ED_i) throughout i waves. We detect PD_i based mostly on the next criterion: a peak’s amplitude is bigger than the third quartile of the incidence time collection and any two native peaks are three months aside. Following the height date detection, we estimate the beginning and ending dates for the waves. For the primary wave, we determine the beginning date as to when the adjustments within the variety of confirmed instances flip to a optimistic integer. For the next waves, we determine the beginning date such that its amplitude h₂ meets the next situation (Eq. (2)).

Illustrating COVID-19 knowledge processing and waves characterization.

H₂ is the height’s amplitude of the non-first wave (Fig. 4). h is the bottom amplitude between this peak and the earlier peak (Fig. 4). The beginning date of this non-first wave is outlined as the primary date on which the worth for (h₂–h) is the same as or lower than 5% of (H₂–h) looking out backward from this wave’s peak. The tip date of any wave was decided utilizing the identical heuristic because the beginning date of a non-first wave (Eq. 3). The distinction was that an finish date was the primary date whose worth (h₁–h) is the same as or lower than 5% of (H₁–h) looking out ahead in time from this wave’s peak.

Our wave detection and characterization algorithm yielded two (three) COVID-19 waves for 610 (26) districts, out of 639 districts (Supplementary Fig. 4). Of the 26 districts, we discover districts encompassing two cities—Delhi and Ahmedabad—and others comparatively rural, i.e., urbanization charges lower than 50%. Because the national- and state-level aggregated knowledge stress two COVID-19 waves, our algorithm underscore the significance of understanding patterns at finer spatial scales, the place novel dynamics will be at play. For instance, in Delhi, we estimate three waves however with a bi-modal distribution through the first wave interval of the nation. In different districts, we observe {that a} comparatively decrease variety of instances, with a speckle signature, through the starting of the pandemic led to anomalous wave detection. Consequently, we assume the primary wave includes the estimated first two waves in districts with estimated three waves.

Constructing on the outputs of our algorithm, we concentrate on three metrics⁴⁵: (1) cumulative incidence proportion, (2) temporal incidence fee, and (3) severity ratio. Cumulative incidence proportion (CIP_ij) is a measure of illness danger outlined right here as a ratio of cumulative COVID-19 incidence (I_ij) throughout a wave (i) over complete inhabitants (Pop_j) for a district (j) (Eq. (4)).

Cumulative temporal incidence fee (CIR_ij) is a measure of the rapidity of illness incidence amongst a inhabitants and over a hard and fast time interval (t days) per wave (i) (Eq. (5)).

Lastly, we introduce a severity ratio metric (SR_j) to measure the severity of the second COVID-19 wave in India in comparison with the primary wave (Eq. (6)).

As a preliminary evaluation, we analyze spatial variations in CIP_ij, CIR_ij, and SR_j. First, we examine CIP_ij, and CIR_ij, between the 2 dominant waves and throughout districts to look at spatial consistency in illness danger and charges of illness unfold. Subsequent, we analyze the spatial patterns of COVID-19 wave begin date for the 2 waves to determine main facilities. Lastly, we analyze SR_j metric throughout districts and estimate the common second-wave severity (relative to the primary wave) and related 95% confidence intervals based mostly on bootstrap estimation with 100,000 replications⁴⁶. We famous a big correlation between severity ratio metrics calculated with incidence proportions and incidence charges with a Pearson’s correlation coefficient of 0.91. Consequently, we use incidence charges to look at second-wave severity right here and in our subsequent correlation and regression evaluation.

Past these metrics, we estimate R₀ based mostly on exponential progress fee^47,48, with a gamma distribution for the serial interval, assuming a imply and customary deviation of 4.4 and three days, respectively, for the era time⁴⁹. Utilizing the identical serial interval assumptions, we estimate R_t utilizing a maximum-likelihood estimation⁵⁰, however based mostly on incidence curves based mostly on begin and peak dates of the wave, yielding a median estimate per wave (left( {R_t^mu } proper)). We additionally report district-level common severity ratios based mostly on estimated R₀ and R_t, computed with a practical type per Eq. (6). Nonetheless, owing to knowledge high quality issues, assumptions underlying R₀ and R_t estimations, and our concentrate on COVID-19 incidences in India, we prohibit our detailed evaluation to CIP_ij, CIR_ij, and SR_j (Supplementary Fig. 5 and Supplementary Desk 6).

Correlation and regression evaluation

We use correlation and regression evaluation to characterize basic options of COVID-19 incidence throughout districts, spanning your entire rural-to-urban gradient. Particularly, we concentrate on the associations between COVID-19 incidence metrics and associated key spatial traits, i.e., urbanization, inhabitants density, wealth, and mobility (Supplementary Desk 6 and Supplementary Fig. 6). First, we discover non-linear monotonic associations between COVID-19 incidence metrics and spatial traits by inspecting Spearman’s correlations. Within the course of, we determine key city options related for COVID-19 incidences. We additional look at these associations utilizing extraordinary least squares (OLS) and, after inspecting the presence of spatial autocorrelation, utilizing spatial regression fashions (estimated with spatialreg package deal⁵¹ in R), i.e., spatial lag fashions (SLM) and spatial error fashions (SEM). These spatial fashions account for potential bias and inconsistencies in OLS estimates as a consequence of spatial autocorrelations⁵² (Eqs. (7) and (8)). In our evaluation, we management for state-level variations, to account for reporting bias³⁴, and interpret the mannequin with the most important log-likelihood estimate and lowest Akaike Data Criterion (AIC) metric between OLS, SLM, and SEM. Lastly, we report Bayesian Markov Chain Monte Carlo estimates⁵¹ for the chosen spatial fashions, as a robustness verify.

The place, Wy spatially lagged final result variable for spatial weights matrix W, ε is the error time period, and ρ and β are the mannequin parameters.

The place, ε is the spatial autocorrelated error phrases, υ are independently and identically distributed errors, and λ and β are the mannequin parameters.

Moral approval

In session with the workplace of the Institutional Evaluate Board (IRB), Human Analysis Safety Program at Princeton College, we decided that an moral approval was not required for our analysis based mostly on the human topics analysis definition and scope.